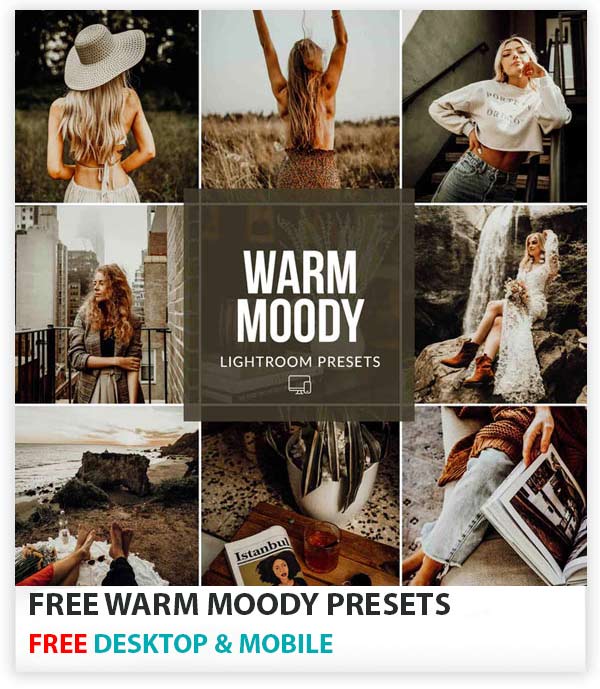
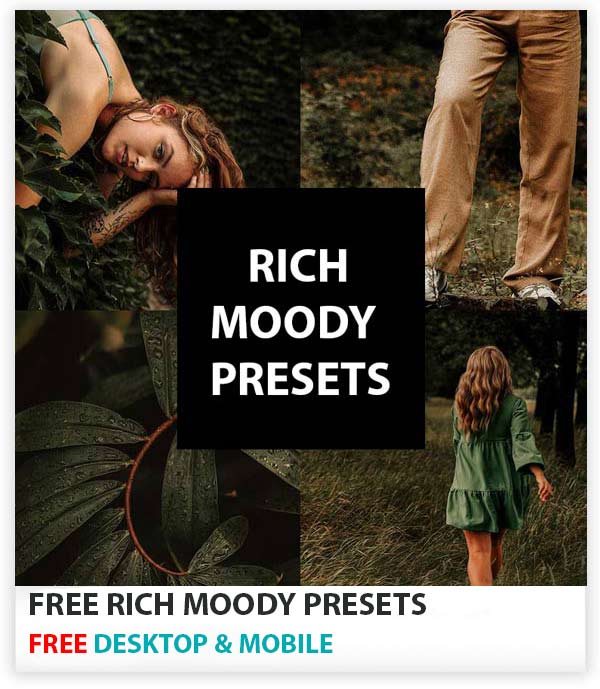
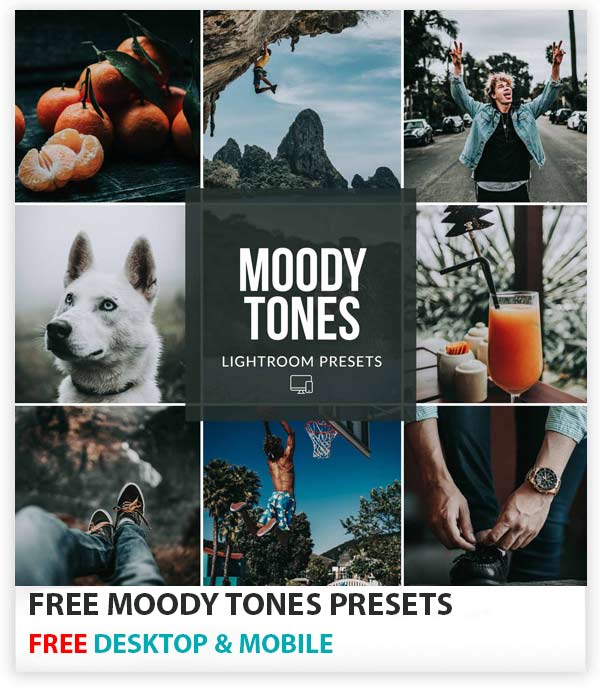
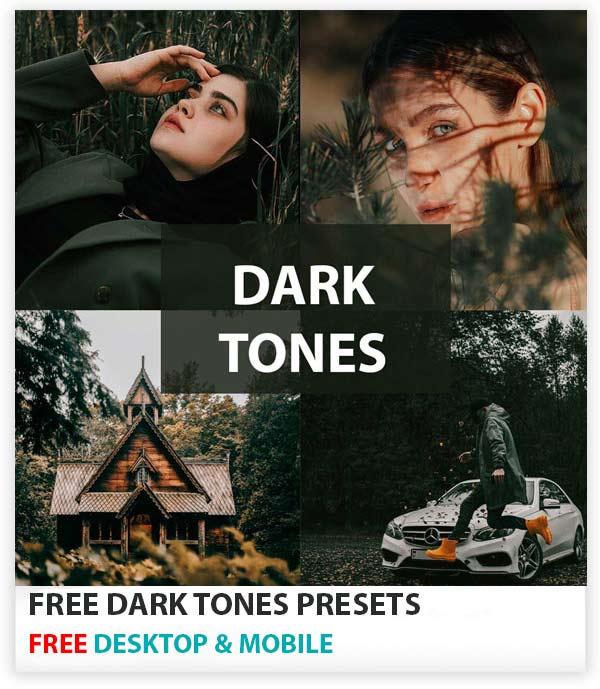
Download my free moody Lightroom presets that will give your photos dark & moody looks in just one click. These presets really gonna give your images beautiful dark, faded & saturated effects making your images ready to tell a story.
You can add dramatic effects, saturated dark moods, muted tones and our presets carefully increase brightness, add warm tones and give a moody feel to images while protecting skin tones. Beautiful warm tones, rich colors, enhanced contrast and much more you can do with these presets.
Note: This pack now includes presets for Lightroom Mobile and it includes presets in the .DNG format.
Take a look at the GIF below to see what types of effects they can quickly add to your image:
Dark & Moody effect in no time to add dramatic feel so you images can narrate a story.
Get Free Lightroom Presets!
Get Free Lightroom Presets including Light & Airy, Dark & Moody, Landscape & many more. Subscribe and get the bundle delivered to your inbox!
These presets will bring the exposure down and you’ll have dark tones in your image as you see in the before/after imagery below. You gotta set the exposure for every image to get the best out of this pack.
Sometimes the presets will give you a high contrast moody look. But don’t worry you can easily create a soft moody look by reducing the contrast. You can also increase the shadows levels for soft effect using the Curve Tool. Download the presets below to get started with that moody look.
Please Note: This pack includes only 1 moody preset in .DNG, .LRTEMPLATE and .XMP format.
Download The Free Moody Preset Here
Get Premium Moody Presets W/ Ultimate Presets Bundle
Check out more Free Mobile Lightroom Presets
thnk u so much
Seems like you are enjoying my freebies Paula!
I just don’t know how to download it , 🤦🏻♀️
Hey, Click on the Download Presets button to download the presets.
How to apply on images ??
You have to install the preset on mobile, you can use this guide here: https://www.psdstack.com/photoshop-tutorials/how-to-install-lightroom-presets/
I saw the guide but the problem is I can’t select the presets from the folder
Make sure you have the presets downloaded to your mobile.
Thanks
Bro i can’t download the preset bro
Thank so much for the presets
Love it!! Justo what I needed!!!
I think this is awesome presets
Plz download
Click on the download button to download the presets.
These are awesome! Thank you Bunty!
Thanks Gwyn! Keep an eye on your email for more freebies!
Thank you so much ❤
You are welcome Swapnil!
Thankyou to u happy new year💥💫
thank you so much
You are welcome Joel!
Wow, I just now applied these presets on my mobile, and the presets are very good. thanks
You are welcome, Sanjeel. A quick tip, after applying any preset, bring down the exposure further to get a dark moody toning.
Bro i cant open it,help me plz
Hey,
It’s a zip file, you’ll need winrar to extract it. Please download the winrar and then extract all the presets.
Thanks,
Bunty
It was amazing.. Thanks brother
You are welcome!
Thankyouu so muchhh!! <3
You are welcome!
I’ve tried downloading it but nothing happened. I even downloaded winrar (zip extractor) still the same issue . Help me out please
Hi Laura,
After clicking on the download button, you should be able to download the presets. I just checked and they downloaded fine to me.
Thanks,
Bunty
Hi !
Yh I’ve been able to download the presets , but after that, I can’t open it. The file is empty .
Oh, I see. As far as I know, they are not empty. Maybe you have an incomplete download. Either way, I have sent them to your email. I hope this resolve the issue.
Thanks,
Bunty
Thank you so much for sharing
Downloaded, but how to use in light room ? 😥
Hey,
You have to install the presets in Lightroom. Follow this guide on how to install presets: https://www.psdstack.com/photoshop-tutorials/how-to-install-lightroom-presets/
Thanks,
Bunty
I have downloaded it and extracted it but when I follow instructions on how to add it in lightroom there are no images or folders that were downloaded. I have no idea where these presets are in my phone….
Hi Samantha,
I am sorry for the inconvenience. You’ll find three folder inside it as you can see here: https://www.dropbox.com/s/1cy90c12wd6crtx/samantha-1.jpg?dl=0 and inside the Mobile folder you’ll find the presets for mobile as you can see here: https://www.dropbox.com/s/b4pqw65grx2bj13/samantha.jpg?dl=0
Please make sure you have located them in your mobile or desktop after the extraction.
Let me know if you have questions!
Thanks,
Bunty
Best presets!
It showing they are either duplicate or invalid when trying to import in Lightroom.
Thank you for the presets!
I have downloaded the presets but the images are not showing up. Please help me 😔
Please find the mobile folder.
Thanks 😊👍
Guys, I don’t know how to apply the presets. Can you help me please? Thank you
Hi Janssen,
Please follow this guide: https://www.psdstack.com/photoshop-tutorials/how-to-install-lightroom-presets/
Thanks,
Bunty
Thank you so much Bunty !!
Glad, you like the moody presets.
I click on the link in the email and nothing happens, comes up blank? 😞
You can try downloading it with a different browser.
Bro password please
Thank you so much for sharing!
I can’t get the presets in my email please help me with this
Wait a minute or two as I have already said that it takes time to deliver the email. You should have the download link by now.
Thank you for amazing presets!! 👊
You are welcome!
How to download
Please subscribe and the download link will be sent to your email.
I want to try this
Thank you so much sir,I’m gonna try em
You are welcome!
Thanks for this beautiful ones
The mobile folder is empty. There are 0 files in it.
No, it’s not. Please download the presets again.